distribute n balls of m colours in r boxes Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the . Shop Junction Box Electrical Enclosure: Steel, NEMA 3R at MSC Direct top provider of high quality products
0 · probability n balls m boxes
1 · n balls vs m boxes
2 · m balls on n boxes
3 · indistinguishable balls on n boxes
4 · how to distribute n boxes
5 · how to distribute m on n
6 · how to distribute k balls into boxes
7 · distributing balls to boxes
No, Lowe’s does not cut metal sheets. However, they do offer cutting services for other materials such as metal rods, chains, wood pieces, and metal pipes. Some locations provide free pipe trimming and threading for galvanized and black metal pipes, with .

Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. .I want to distribute n labeled balls into m labeled boxes. I know one obtains the .distribute k indistinguishable balls into n distinguishable boxes, without exclusion. We should discuss another condition that is commonly placed on the distribution of balls into boxes, .Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the .
Distribute $a + b + c$ distinct balls into boxes $A, B, C$ such that $a$ balls, $b$ balls and $c$ balls go to boxes $A, B, C$
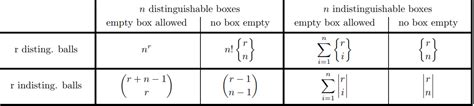
Given an array arr[] of size N, representing the number of balls of each of N distinct colors, the task is to find the probability of distributing all the balls into two boxes, such . The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, .
Let's say you have a group of M M balls of different colors in a box. For example, 20 balls are red, 15 are blue, 10 are green, 5 are grey, 5 are yellow and 5 violet, for a total of M .Probability of a Two Boxes Having The Same Number of Distinct Balls - Given 2n balls of k distinct colors. You will be given an integer array balls of size k where balls [i] is the number of . I want to distribute n labeled balls into m labeled boxes. I know one obtains the number by $m^n$. But I don't quite understand why. The underlying argument is always I have .When distributing n indistinguishable balls into m distinguishable boxes, the total number of ways can be calculated using the formula: $$C(n + m - 1, m - 1)$$. If each box can hold any number .
probability n balls m boxes
Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. For example, one way is that all $N$ balls land in one box.distribute k indistinguishable balls into n distinguishable boxes, without exclusion. We should discuss another condition that is commonly placed on the distribution of balls into boxes, namely, the condition that no box be empty.Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the balls are distributed in the boxes we use $N-1$ "|".
Distribute $a + b + c$ distinct balls into boxes $A, B, C$ such that $a$ balls, $b$ balls and $c$ balls go to boxes $A, B, C$ Given an array arr[] of size N, representing the number of balls of each of N distinct colors, the task is to find the probability of distributing all the balls into two boxes, such that both the boxes contain an equal number of distinct colored balls. The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, and 1 - in this case M=4 and N=3). Let's say you have a group of M M balls of different colors in a box. For example, 20 balls are red, 15 are blue, 10 are green, 5 are grey, 5 are yellow and 5 violet, for a total of M = 60 M = 60 balls. You pick 1 ⩽ n ⩽ M 1 ⩽ n ⩽ M of them without replacement.
Probability of a Two Boxes Having The Same Number of Distinct Balls - Given 2n balls of k distinct colors. You will be given an integer array balls of size k where balls [i] is the number of balls of color i.
I want to distribute n labeled balls into m labeled boxes. I know one obtains the number by $m^n$. But I don't quite understand why. The underlying argument is always I have m choices for the first ball m choices for the second and so on. As an example lets take 3 balls labeled A,B,C and two boxes 1,2
When distributing n indistinguishable balls into m distinguishable boxes, the total number of ways can be calculated using the formula: $$C(n + m - 1, m - 1)$$. If each box can hold any number of balls (including zero), this scenario fits perfectly within the framework of .Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. For example, one way is that all $N$ balls land in one box.
how to ground receptacle to metal box
distribute k indistinguishable balls into n distinguishable boxes, without exclusion. We should discuss another condition that is commonly placed on the distribution of balls into boxes, namely, the condition that no box be empty.Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the balls are distributed in the boxes we use $N-1$ "|". Distribute $a + b + c$ distinct balls into boxes $A, B, C$ such that $a$ balls, $b$ balls and $c$ balls go to boxes $A, B, C$
how to hide electric transformer box in yard
Given an array arr[] of size N, representing the number of balls of each of N distinct colors, the task is to find the probability of distributing all the balls into two boxes, such that both the boxes contain an equal number of distinct colored balls. The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, and 1 - in this case M=4 and N=3). Let's say you have a group of M M balls of different colors in a box. For example, 20 balls are red, 15 are blue, 10 are green, 5 are grey, 5 are yellow and 5 violet, for a total of M = 60 M = 60 balls. You pick 1 ⩽ n ⩽ M 1 ⩽ n ⩽ M of them without replacement.
Probability of a Two Boxes Having The Same Number of Distinct Balls - Given 2n balls of k distinct colors. You will be given an integer array balls of size k where balls [i] is the number of balls of color i. I want to distribute n labeled balls into m labeled boxes. I know one obtains the number by $m^n$. But I don't quite understand why. The underlying argument is always I have m choices for the first ball m choices for the second and so on. As an example lets take 3 balls labeled A,B,C and two boxes 1,2
n balls vs m boxes
m balls on n boxes
He has just posted the results of his quick and dirty testing of a Conex box (shipping container) as a Faraday cage. His tests revealed that the Conex box will act as a partial Faraday cage. All who are interested in protecting electronics really owe it to themselves to buy his book about EMP/CME.
distribute n balls of m colours in r boxes|how to distribute k balls into boxes